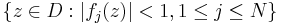Analytic polyhedron
In mathematics, especially several complex variables, an analytic polyhedron is a subset of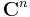 
of the form
where 
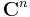is a bounded connected open subset of and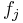 
are holomorphic on D.[1] If 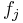above are polynomials, then the set is called a polynomial polyhedron. Every analytic polyhedron is a domain of holomorphy (thus, pseudo-convex.)
An analytic polyhedron is a Weil domain.
See also: the Behnke–Stein theorem.
References
- Lars Hörmander. An Introduction to Complex Analysis in Several Variables, North-Holland Publishing Company, New York, New York, 1973.